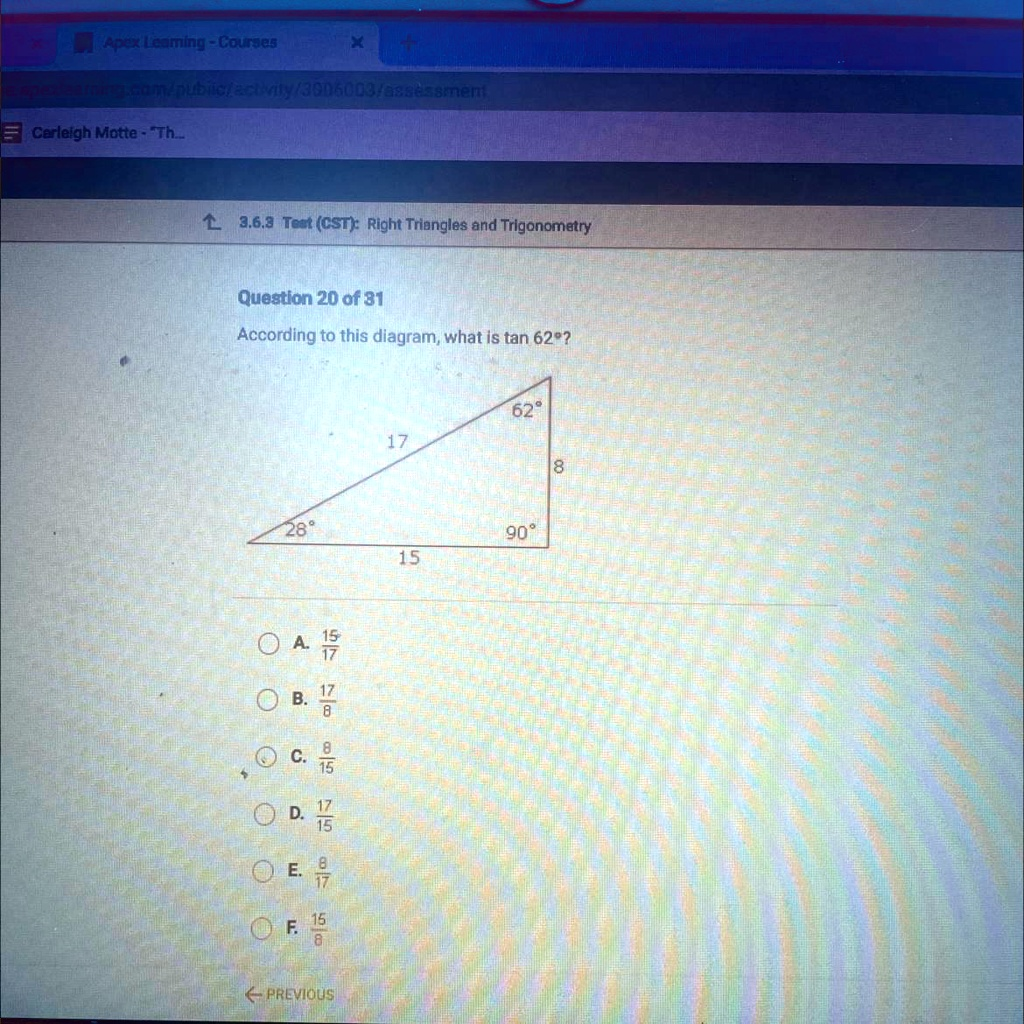
Apex Leaming – Courses X + a.com/public/activity/3006003/assessment Carleigh Motte – “Th… ?3.6.3 Test (CST): Right Triangles and Trigonometry Question 20 of 31 According to this diagram, what is tan 62°? 62° 17 28° 15 15 A. 17 B. 17 C. 8 8 D. 17 15 E. 17 F. 15 8 ? PREVIOUS 90° 8
The Correct Answer and Explanation is:
To solve the question “According to this diagram, what is tan 62°?”, we need to use the definition of the tangent function in trigonometry.
Step-by-step explanation:
In a right triangle:tan(θ)=oppositeadjacent\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}tan(θ)=adjacentopposite
From the triangle shown in the image, for angle 62°:
- Opposite side to 62° = 8
- Adjacent side to 62° = 15
So,tan(62∘)=815\tan(62^\circ) = \frac{8}{15}tan(62∘)=158
Answer:
✅ Option C: 815\frac{8}{15}158
explanation:
In trigonometry, the tangent of an angle in a right triangle is a ratio comparing the length of the side opposite the angle to the length of the side adjacent to the angle. This definition comes directly from the properties of right triangles and is one of the primary trigonometric functions.
In this problem, you are given a right triangle with a 62° angle and asked to find the value of tan(62°) based on the diagram. To do this, first identify the side opposite the 62° angle and the side adjacent to it. According to the diagram, the side opposite 62° is labeled as 8 units, and the side adjacent to 62° is labeled as 15 units. Using the definition of tangent, you substitute these values into the formula:tan(62∘)=oppositeadjacent=815\tan(62^\circ) = \frac{\text{opposite}}{\text{adjacent}} = \frac{8}{15}tan(62∘)=adjacentopposite=158
You do not need to use a calculator or look up tangent values in a table for this problem, because the triangle has already been labeled with the exact side lengths that correspond to the 62° angle. This simplifies the work and makes it a straightforward application of the tangent ratio.
Therefore, the correct value for tan(62°) based on the triangle is 8 divided by 15. Among the options given, this matches choice C.
Understanding and applying these definitions helps in solving many triangle problems without needing advanced tools or memorized values.
