Triangle DEF is an isosceles triangle. Find
.
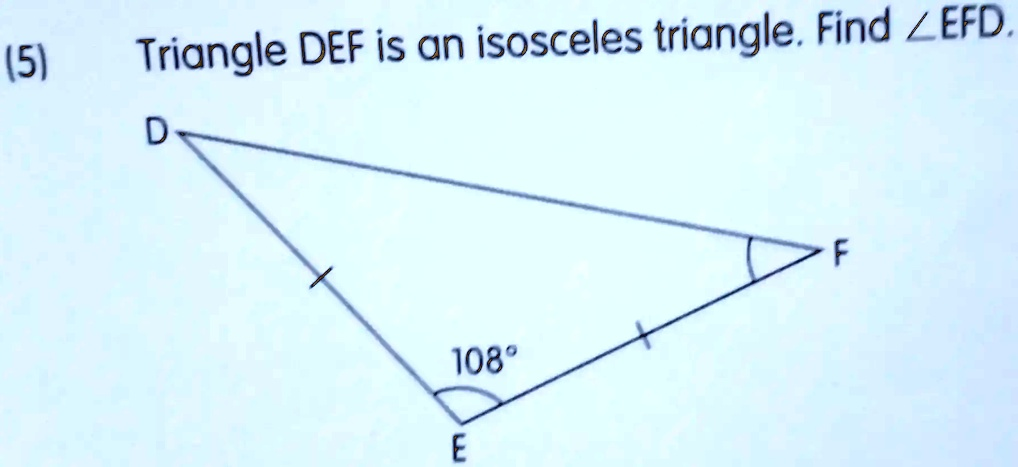
The Correct Answer and Explanation is:
To find the measure of angle ∠EFD in triangle DEF, observe that DE is equal to DF, so the triangle is isosceles with equal base angles at ∠EFD and ∠DEF. The given angle at vertex E is 108°.
Let ∠EFD = ∠DEF = x.
By the angle sum property of a triangle:
x + x + 108° = 180° 2x + 108° = 180° 2x = 72° x = 36°
Therefore, the measure of angle ∠EFD is 36°.
Explanation:
Triangle DEF is specified as isosceles, with DE equal to DF. This tells us that the angles opposite those equal sides—namely ∠DEF and ∠EFD—are also equal. When confronted with such a configuration, it becomes natural to assign a variable to the unknown base angles, say x degrees each, to simplify the calculation.
The key geometric principle applied here is that the interior angles of any triangle must add up to exactly 180 degrees. With the apex angle ∠EDF given as 108 degrees, the sum of the other two angles must be 180° minus 108°, which is 72°. Because the base angles are equal, we divide 72° evenly between them.
Mathematically, this results in two equations:
- x + x + 108° = 180°, combining the known angle with the two unknown but equal base angles
- Solving that gives 2x = 72°, hence x = 36°
What makes this example a classic in geometry is how it combines symmetry and algebra to reveal hidden properties. Problems like this develop intuition for angle relationships in polygons, and reinforce how geometric reasoning can lead to precise numerical conclusions.
Using visual clues like equal sides or angle marks can often guide the approach, making it easier to set up the right equations and arrive at a confident solution.
