X X X xlx X X YxxKkx B Xkxxxxi X XXXXXXXX XX XX XX>XXyx X B xAxxxxix XX Xy XxXX
The Correct Answer and Explanation is:
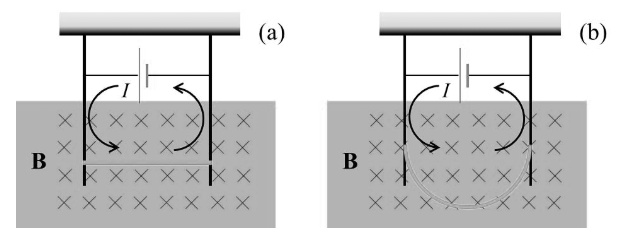
Based on the uploaded diagrams, we are analyzing the interaction of a rectangular current-carrying loop with a uniform magnetic field directed into the page. Diagram (a) shows the loop at rest, while diagram (b) depicts it moving to the right. The key to interpreting the cryptic symbols is understanding the physics illustrated.
Correct Answer:
In diagram (a), there is no net magnetic force or torque on the loop, since the magnetic forces on opposite sides of the loop cancel symmetrically due to the uniform magnetic field and the stationary loop.
In diagram (b), the loop is moving to the right. This motion introduces motional emf due to the interaction between the velocity of the loop and the magnetic field. As the loop moves, induced currents arise, and a net magnetic force acts on it. Specifically, Lenz’s Law dictates that the induced current will oppose the change—here, it will act to resist the loop’s rightward motion.
Explanation:
The diagrams highlight fundamental aspects of magnetic forces on current-carrying conductors and electromagnetic induction. In diagram (a), with the loop at rest in a uniform magnetic field, each segment of the loop experiences a force given by F = I (L × B). However, the symmetry ensures these forces cancel in pairs. The top and bottom segments generate forces equal in magnitude but opposite in direction. The vertical sides also cancel due to equal length and opposite currents.
In diagram (b), as the loop moves rightward, the interaction between its velocity v and the magnetic field B generates an induced emf: emf = vBL for each moving segment. This results in an induced current whose magnetic interaction with B creates a net force opposing the motion, a manifestation of Lenz’s Law. The loop effectively behaves like a basic generator, where motion through a magnetic field induces a current.
This concept underlies devices like electric generators and rails in maglev systems, where motion and magnetic fields interact to produce electrical effects.
