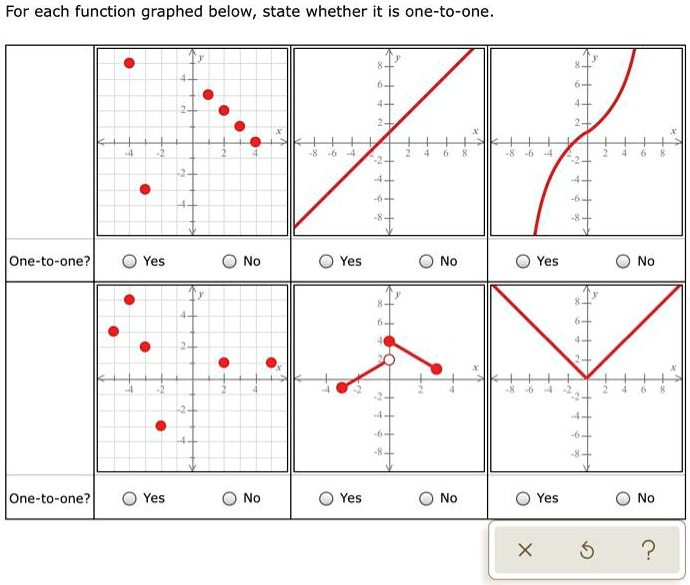
For each function graphed below,; state whether it is one-to-one

For each function graphed below,; state whether it is one-to-one One-to-one? Yes Yes No Yes One-to-one? Yes Yes No Yes X 2

The Correct Answer and Explanation is:

Here is the correct identification of whether each graphed function is one-to-one:

Top Row (from left to right):

1. No
2. Yes
3. No

Bottom Row (from left to right):

4. No
5. No
6. Yes

A function is considered one-to-one if every element of the range corresponds to exactly one element of the domain. Put another way, no two different x-values can produce the same y-value. The most common method to test for this is the horizontal line test. If any horizontal line intersects the graph more than once, the function is not one-to-one.

Let’s explore each case:

• Graph 1 (Top Left) appears to be a scatter plot without a consistent trend. Since several points share the same y-value with different x-values, the graph fails the horizontal line test. Therefore, it is not one-to-one.
• Graph 2 (Top Middle) is a straight line with a positive slope. It passes the horizontal line test because no horizontal line intersects it more than once. This graph represents a one-to-one function.
• Graph 3 (Top Right) shows a curve that increases and then decreases. This shape guarantees that some y-values are repeated for different x-values, so it is not one-to-one.
• Graph 4 (Bottom Left), another scatter plot, displays similar issues as Graph 1 with repeated y-values. Hence, it is also not one-to-one.
• Graph 5 (Bottom Middle) is a piecewise function with segments that overlap in the vertical sense. Since multiple x-values lead to the same y-value within segments, it fails the test and is not one-to-one.
• Graph 6 (Bottom Right) is V-shaped but tilted diagonally. It passes the horizontal line test, so this function is one-to-one.

Understanding these distinctions sharpens your grasp of function behavior and the geometry behind algebraic relationships.