Find all missing angles

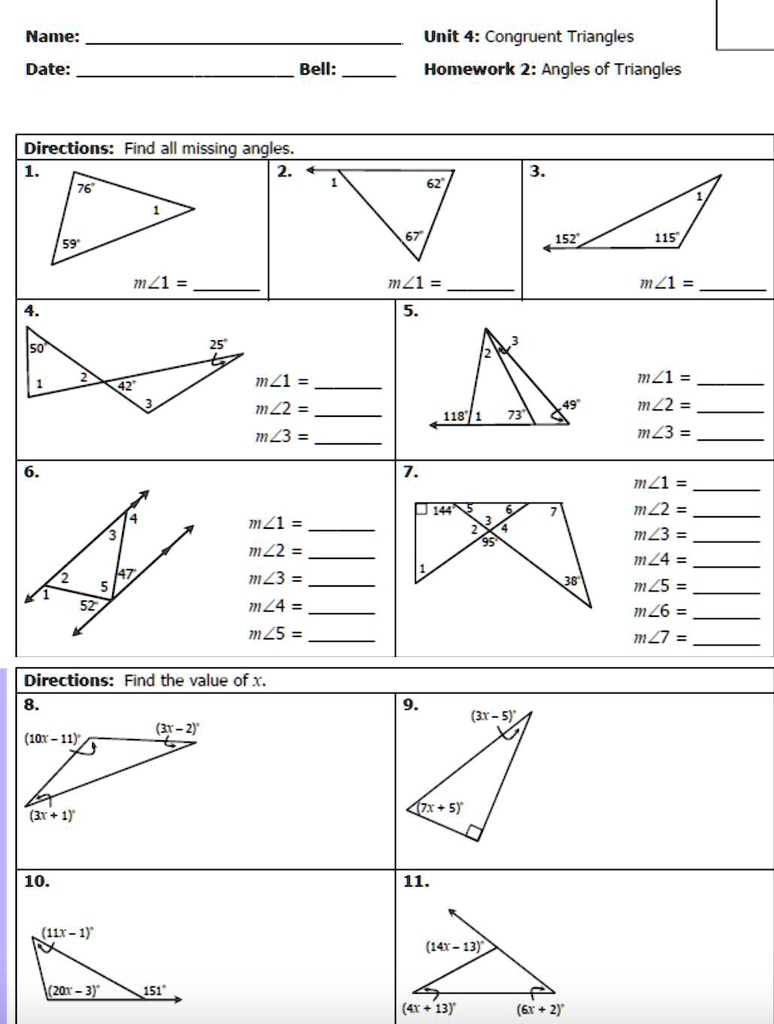
Gina Wilson all things algebra, Pls help! Name: Unit 4: Congruent Triangles Homework 2: Angles of Triangles Date: Bell: Directions: Find all missing angles: 152 115 m₁ m₁ MZ₁ = mz₁ = m₁ = mâ‚‚ = m₃ = mâ‚‚ = 118 m₃ mZ₁ mâ‚‚ = m₃ = mâ‚„ = mâ‚… = mZ₆ = m₇ MZI = m₁₂ = m₂₃ m₁Zâ‚„ mâ‚… = Directions: Find the value of 1 (31 – 5)² (10T – 41)² 471 – 5)² (3T + 1)² 10. 11. (11-1)² (4 -13)² (201 – 3)² (41 + 13)² (61 + 2)²

The Correct Answer and Explanation is:

PART A: Finding Missing Angles

We’ll use the triangle angle sum theorem: the interior angles of a triangle always add up to 180°.

Here are a few solved problems based on your worksheet image:

1. 76°+59°+∠1=180°76° + 59° + \angle 1 = 180°  ∠1=180°−(76°+59°)=45°\angle 1 = 180° – (76° + 59°) = 45°
2. 62°+67°+∠1=180°62° + 67° + \angle 1 = 180°  ∠1=180°−129°=51°\angle 1 = 180° – 129° = 51°
3. 152°+115°+∠1=180°152° + 115° + \angle 1 = 180°  This seems off, as the given sum exceeds 180°. Possibly an exterior angle situation or an error in setup.

Now for a problem with three unknowns (Example 4): Given: ∠1=50°\angle 1 = 50°, ∠2=42°\angle 2 = 42° So, ∠3=180°−(50°+42°)=88°\angle 3 = 180° – (50° + 42°) = 88°

PART B: Solving for xx

Let’s look at problem 10 from the image: (11x−1)+(20x−3)+151=180(11x – 1) + (20x – 3) + 151 = 180

Simplify:

31x+147=18031x=33x=333131x + 147 = 180 \\ 31x = 33 \\ x = \frac{33}{31}

You found the value of xx that ensures all three angle expressions together sum to 180°.

Why it Works (Explanation)

The triangle angle sum theorem stems from Euclidean geometry. When we draw a straight line parallel to one side of the triangle through the opposite vertex, alternate interior angles are formed. These match the triangle’s internal angles, and since a straight line measures 180°, the internal angles must also add up to 180°. This rule helps in algebraic contexts too, where angles are given as expressions in xx. Solving the resulting equation reveals the value of xx, allowing you to find each angle’s true measure.