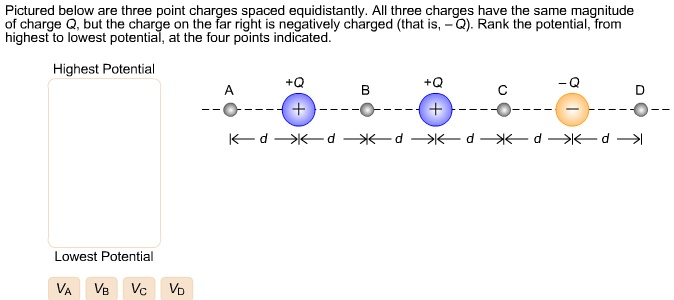
The Correct Answer and Explanation is:
To rank the electric potential at points A, B, C, and D, we consider the contributions from each charge. Electric potential is a scalar quantity, so we sum the potentials due to all charges at each point. The potential VV from a point charge is given by V=kQrV = k \frac{Q}{r}, where kk is Coulomb’s constant, QQ is the charge, and rr is the distance from the charge to the point of interest.
Each charge has the same magnitude, so the sign and distance primarily affect the potential. Let’s evaluate:
- Point B lies directly between the two positive charges. It is symmetrically placed, so the potentials from both positive charges add constructively. The negative charge is farther away and contributes less significantly. Thus, B has the highest potential.
- Point A is to the left of the first positive charge. It is influenced mostly by one nearby positive charge, while the other positive and negative charges are farther. Overall, it has positive potential, though less than B.
- Point C sits between a positive and negative charge. The proximity to both charges means the potentials partly cancel. Since the magnitude is equal and distances are similar, the net potential is lower, possibly close to zero or slightly negative.
- Point D is near the negative charge with little influence from the positive charges due to greater distances. It experiences a net negative potential, the lowest of all points.
Correct ranking from highest to lowest potential:
VB>VA>VC>VDV_B > V_A > V_C > V_D
This ranking reflects the dominance of positive or negative charges at each point, moderated by their distances. Because potential is scalar, it simplifies to additive effects, not vector summation. That is why symmetry and proximity play crucial roles in determining the correct order.
