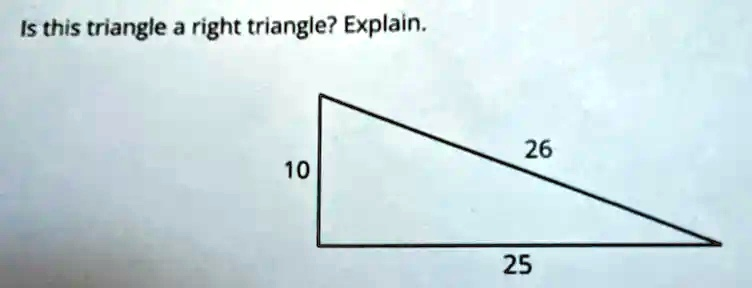
Is this triangle a right triangle? Explain.
The Correct Answer and Explanation is:
No, the triangle with side lengths 10, 25, and 26 is not a right triangle.
To determine this, we apply the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. That is:
c2=a2+b2c^2 = a^2 + b^2
Assuming 26 is the longest side, it would be the hypotenuse. We now test the relationship:
- 102=10010^2 = 100
- 252=62525^2 = 625
- 262=67626^2 = 676
Adding the squares of the shorter sides:
100+625=725100 + 625 = 725
Now compare this with the square of the supposed hypotenuse:
676≠725676 \neq 725
Since the sum of the squares of the two shorter sides is not equal to the square of the longest side, the triangle fails the Pythagorean test. Therefore, it is not a right triangle.
This result reveals more than a simple classification. Understanding whether a triangle is right-angled affects how we analyze it geometrically and algebraically. Right triangles have special properties, such as allowing the use of trigonometric ratios like sine, cosine, and tangent. They also enable certain shortcuts in geometric proofs and constructions.
By contrast, triangles that are not right-angled, like this one, require different strategies. One may instead apply the Law of Cosines to explore angle measurements or determine whether the triangle is obtuse or acute. Moreover, this exercise is a practical example of critical thinking in mathematics. It reminds us that we cannot rely on visual intuition or estimates. Only precise numerical evaluation gives us a definitive answer.
This is why the Pythagorean theorem remains one of the most powerful tools in both theoretical mathematics and real-world applications. When used correctly, it eliminates all guesswork.
