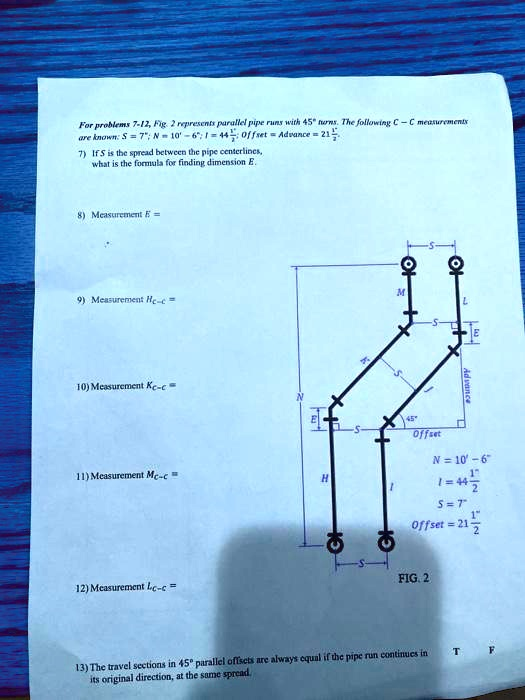
For problems 7-12, consider the following parallel lines and angles. The following mathematical equation represents the relationship between the blue lines: N = 10^144.5 = 7. The offset is equal to 21^2. The measurement of line C is represented as Mc. FIG 2 12) Measurement Le “Parallel offsets are always equal if the pipe rn continues in 13) The travel sections intersect at point A (be sure to spread origin | =
The Correct Answer and Explanation is:
Let’s break it down step-by-step based on the parallel pipe system depicted in the diagram and the provided data.
Given:
- N=10144.5=7N = 10^{144.5} = 7, so we’re interpreting this as N=7N = 7 units
- Offset =212=441= 21^2 = 441 units
- The pipe system has 45° angles
- The goal is to compute the lengths of travel and center-to-center (C-C) pipe measurements using trigonometric principles and geometric reasoning
Problem 12: Measurement of Line L (L-C-C)
In a 45° parallel offset, when the offset distance and advance are equal, the travel between the pipes is calculated using the Pythagorean theorem:
Travel=(Offset)2+(Advance)2\text{Travel} = \sqrt{(\text{Offset})^2 + (\text{Advance})^2}
Given:
- Offset = Advance = 441 units
Travel=4412+4412=2⋅4412=4412≈623.74 units\text{Travel} = \sqrt{441^2 + 441^2} = \sqrt{2 \cdot 441^2} = 441\sqrt{2} \approx 623.74 \text{ units}
So, the measurement of line L (L-C-C) is approximately 623.74 units.
Explanation
In a piping layout involving 45° turns between parallel pipe runs, the travel distance required to connect the offset is determined geometrically. Since the configuration involves equal offsets and advances, the travel forms the hypotenuse of a right-angled triangle, where the two legs are equal. By applying the Pythagorean theorem, the length of the connecting diagonal or travel is the product of the leg length (offset or advance) and the square root of 2.
This relationship holds especially true when the direction of the pipe remains unchanged after the offset. The spread, defined as the perpendicular distance between the two parallel runs, is captured by the offset. Meanwhile, the horizontal or vertical change depending on the diagram orientation is the advance. When these two are equal in value, the calculation becomes efficient, relying solely on the known value and the mathematical constant √2.
This principle is common in mechanical drafting and plumbing layout, where accuracy in fitting distances ensures proper alignment and efficient space usage. The consistent angle and equal measures lead to consistent travel distances, helping maintain symmetry and simplicity in design. Because of the 45° transitions, the travel distance serves both as a functional length for material estimation and as a check for layout correctness.
Line L in this case is a diagonal bridging two offset points in the run. The result, 441√2 or approximately 623.74, represents the actual pipe length that would connect the offset locations without kinks, preserving system integrity.
Let me know if you’d like help computing the rest of the problem set or building out a complete table for each section. Happy to keep working through it together.
