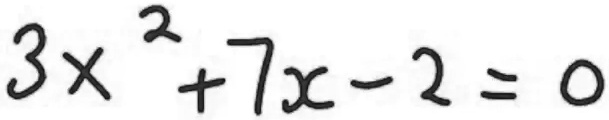
The Correct Answer and Explanation is:
To solve the quadratic equation 3x² + 7x − 2 = 0, we apply the quadratic formula:
x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}
Here, the coefficients are:
- a=3a = 3
- b=7b = 7
- c=−2c = -2
Substitute into the formula:
x=−7±72−4(3)(−2)2(3)=−7±49+246=−7±736x = \frac{-7 \pm \sqrt{7^2 – 4(3)(-2)}}{2(3)} = \frac{-7 \pm \sqrt{49 + 24}}{6} = \frac{-7 \pm \sqrt{73}}{6}
Thus, the two solutions are:
x=−7+736andx=−7−736x = \frac{-7 + \sqrt{73}}{6} \quad \text{and} \quad x = \frac{-7 – \sqrt{73}}{6}
This equation exemplifies a typical quadratic where solutions are irrational. The quadratic formula is effective regardless of whether the roots are rational, irrational, or complex. The expression under the square root, called the discriminant, is critical to understanding the nature of the solutions. In this case, the discriminant is 73. Since it is positive but not a perfect square, the solutions are real and irrational.
Quadratic equations like this appear in various contexts: physics for modeling trajectories, economics for analyzing cost functions, and biology in population models. Recognizing the standard form ax2+bx+c=0ax^2 + bx + c = 0 and being able to extract coefficients for substitution into the quadratic formula is a fundamental algebraic skill.
While factoring is preferred when possible for its simplicity, some equations like this one resist easy factorization due to irrational roots. Hence, mastering the quadratic formula ensures accuracy and completeness when simpler methods fall short. This problem reinforces the importance of algebraic precision and highlights how formulas serve as reliable tools across mathematical disciplines.
